Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ instead of $(T+S)(u)$ and $(T)(u+v)$? - Mathematics Stack Exchange

I am reading Linear Algebra Done Right and want to prove that $L(V, W)$ is a vector space. I have read the solution here: Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ inst

Solved Given vectors U7, , up and w in V, show that w is

Proving a function is a linear map - Mathematics Stack Exchange

Solved (a) Give an example (with proof) of a linear map

Solved 1.8.28 Question Help Let u and v be vectors in Rn. It

JRFM, Free Full-Text

Proving that a Linear Transformation of a Subspace is a Subspace - Mathematics Stack Exchange

Subgrid modelling for two-dimensional turbulence using neural networks, Journal of Fluid Mechanics

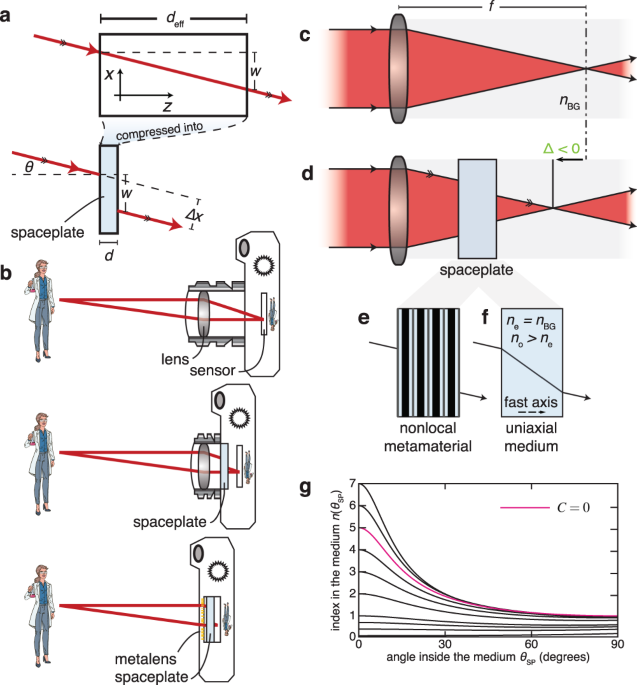
An optic to replace space and its application towards ultra-thin

Solved Theorem 1. Let T:V + W be a linear transformation. T

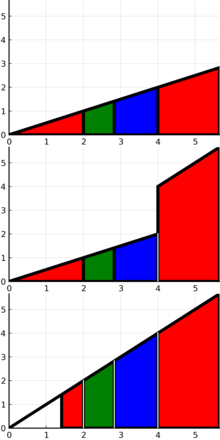
Geometric series - Wikipedia

Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ instead of $(T+S)(u)$ and $(T)(u+v)$? - Mathematics Stack Exchange